逐次近似法で非線形方程式を解く[C言語]

先日ブックオフにて古めかしい『情報処理入門コース7　数値計算』という本が200円で売られていた。こういう専門書とかは古くて汚れてても内容がしっかりしてるから，なかなか安くなっとる奴がないんですわ。

こういった経緯があって，せっかく衝動買いしたのでFortranで書かれたコードを自分なりにC言語で書きなおして読んでいこうと思う。

前置きはここまでにして早速本題へ。
逐次近似法 ( successive approximation method ) で非線形方程式を解くって言ったけれども，ざっくり言うと漸化式を計算するだけ(厳密な説明は省略)。高校とかでやってた「この数列の極限は～」の応用みたいなもの。でもちゃんと解けるからすごい。

今回は次の方程式を解いてみようと思います。

本の方程式とは違うやつにしたかっただけで，特に意味は無い。この式が0となるxを求めていきます。

1.漸化式を作る

すべての方程式で使えるというわけではないが，次のプロセスでだいたい漸化式ができる。
まずx=の形をとりあえず作る

で，それっぽくすれば漸化式の完成。

これが正しいかどうかは解との差が収束するかどうかを証明しなければならないのだが，なれない数式入力にギブアップ。こいつの極限が解に近づくという前提ですすめます。

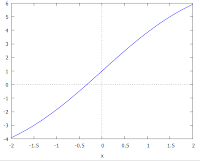
2.グラフを書いて解の目星をつける

逐次近似法の悪いところは最初にどの辺に解があるかの目星をつけなければならないところ。場合によっては解に収束しないということがあります。

拡大して見ていただくと分かる通り，大体-0.3ぐらいでx軸に交わっている事がわかります。なので解はおおよそ-0.3だろうという前提ですすめていきます。

3.漸化式を計算する

数列Xnの初期値X1=-0.3として計算を始める。プログラムは以下の通り。

/**
 * main.c
 * 2015/09/29
 * モンテカルロ法で円周率を求めるプログラム
 */

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

/* 試行回数 */
#define N 100000

/* ランダムに点を決め，円の中なら1，そうでなければ0を返す */
int step(){
 double x,y;
 
 /* x,yに0から1の乱数を代入する */
 x = (double)rand() / ( RAND_MAX + 1);
 y = (double)rand() / ( RAND_MAX + 1);
 
 /* 原点からの距離の二乗が1未満なら円の中 */
 if( x * x + y * y < 1 )
  return 1;
 
 return 0;
}

int main(void){
 int i;
 int m = 0;
 
 /* 乱数の種をまく */
 srand(time(NULL));
 
 for( i = 0 ; i < N ; i++ ){
  /* 点が円の中なら */
  if( step() == 1 ){
   /* mを1増やす */
   m++;
  }
 }
 
 /* 結果を出力する */
 printf("pi = %lf\n", 4.0 * m / N );
  
 return 0;
}

このプログラムを実行するとx = -0.335420となる。THRESHOLDをもう少し小さくすればもうすこし精度は上がるが，丸め誤差があるからあまり小さくすると収束しなくなるのでお気をつけて。

実際にf(-0.335420)を計算すると-5.793E-6となりほぼ0に等しいことがわかります。
まぁ以上が大方の流れです。この後漸化式の証明と，誤差の評価とかをしなくちゃならないが，そこら辺は難しそうな本とか他のサイトに任せます。